Pitch: Slicing up infinity
The electromagnetic spectrum covers a huge span of wavelengths, from a trillionth of a meter to (hypothetically) the size of the universe. Most of this energy — gamma rays, X-rays, microwaves, ultraviolet, and so on — is invisible. But a tiny sliver is visible light:

Different wavelengths within that tiny window present as different colors. Newton first described the rainbow as having five colors — purple, blue, green, yellow, and red. He later added orange and indigo for a silly reason I’ll describe in a minute. Neither answer was wrong, and neither was right.
When I was six, my box of crayons had eight colors. By the time I was ten, there were 64. The crayonic scientists hadn’t discovered 56 more colors — they just split the spectrum into finer divisions, adding colors like blue-green and green-blue. (Some speak of a 120-color Crayola box, but the few photos that exist are suspiciously blurry.)
My first color computer monitor displayed 256 colors. The one I’m on now has the weirdly non-specific “millions of colors.” The possible colors in that spectrum are literally infinite: Just as you can endlessly divide a number line into smaller and smaller fractions, you can tweak wavelengths forever. So instead of being handed a specific natural palette, we divide the spectrum up arbitrarily to meet our needs: five colors in the rainbow, or seven; eight crayons or 64; 256 colors on the monitor, or millions; and 1500 choices in the Sherwin-Williams store. Until you mix a speck of mauve into the gallon of Carnival Orange and get 1,501.
Sound works the same as color. The range of frequencies we can hear is a sliver of the possible range of vibrations. Here’s the full range that the average human can hear, from 20Hz to 20,000Hz:
[arve url=”https://www.youtube.com/embed/qNf9nzvnd1k” /]
Like color, pitch is infinitely divisible, so we make choices about how finely to slice up that spectrum of sound. But one division is so basic to the physics of sound that it serves as the starting point for pretty much every music system on Earth: the octave. Give us an octave, Dorothy:
[arve url=”https://www.youtube.com/embed/PSZxmZmBfnU” parameters=”start=0 end=3″ /]
Doubling any vibration sends you up one octave, and the octave is the relationship between any note and its first overtone. It’s the strongest pitch relationship in music, and you can hear the family resemblance. In Western music, we designate that close relationship with a letter name. Notes vibrating at 110, 220, 440, and 880Hz are all “A,” for example.
So octaves are basic. But using octaves as the only musical steps would make for pretty poor music, like painting with 50 shades of grey. We want additional pitches to use, smaller divisions to give us more of the available colors. How small is the question.
There’s a slightly hilarious psych term for the amount something has to change before the average person will notice. You’d think it would be the “minimum discernment threshold” (MDT) or something similarly sciencey, but no: It’s the JND — the Just-Noticeable Difference. When my wife gets a haircut, it’s often a JND experiment for me.
The concept reaches even beyond haircuts to the perception of things like color and pitch.
That audible range from 20Hz to 20KHz is about 10 octaves. (For comparison, the piano keyboard is just over 7 octaves.) We could split the full range of human hearing into a maximum of about 1,400 just-noticeably-different pitches — 140 pitches per octave. But just as octaves are too big to be our only interval, these are way too small to make musical sense. Going from one to the next sounds more like drifting very slightly out of tune than anything musically useful.
So over time, instead of using 140 pitches in the octave that are barely noticeable in their differences, music cultures have divided up the octave into fewer, more useful and noticeable pitch differences.
South Indian Carnatic music uses the term śruti (or shruti) for the smallest meaningful interval of pitch. Some Carnatic theorists have put that number as high as 66 pitches in the octave, but Carnatic practice actually uses 22 — still a lot of small steps to Western ears. The result is some amazingly nuanced, slippery melodic contours.
Listen to the tiny pitch differences in this performance. The string drone establishes a central pitch, like the Western tonic. The singer’s voice dances in the amazingly tight Carnatic spaces around that center. Just before the midpoint of the clip, she locks in with the drone, then dances away again, returning home once more at the end (58sec):
[arve url=”https://www.youtube.com/watch?v=s5a3pthL_tU” parameters=”start=9 end=75″ /]
Western music settled on 12 pitches, equally spaced about twice as far apart as the Carnatic śruti:
That’s the arbitrary paint store that provides pitches for nearly all Western music — folk tunes, opera, rock, pop, everything. It’s called a chromatic scale, which is perfect — chroma is Greek for color, and scala is Italian for ladder or steps. It isn’t music any more than a paint store is a painting. It’s the resource we draw on to create music.
As the Carnatic example shows, the octave can be divided up any number of other ways. There are big gaps between those notes in the chromatic scale, and there could be notes in those spaces, or in some of those spaces but not others. The composer Harry Partch built his own instruments to bust out of the constraints of the Western pitch ladder. Try this on for a minute:
Several more recent inventions like the fluid piano and tonal plexus have also poked around in those pitch gaps. (If you love this kind of boundary-pushing, find 17 minutes for this stunning soundscape by Wendy Carlos.)
Instead of finding more pitches in the cracks of the chromatic scale, we usually go the other way, taking pitches away from the 12 and playing around with what remains. You can get a scale with steps of various sizes that way. Even the 22-pitch Carnatic system doesn’t treat all 22 as equal players in a given piece. There’s a subset that provides the melodic backbone, and the rest serve as ornaments and variants.

Newton’s wheel, with colors analogous to pitches in the major scale. Different-sized pie wedges equal different intervals in the scale.
The Western major scale works the same way, using seven of the 12 pitches as the backbone of melody and harmony — that’s your do re mi fa sol la ti. The other five pitches are “non-diatonic,” meaning outside of the key, and are used as ornaments and variants — delightful, delicious ornaments and variants.
The seven-note major scale, by the way, is why Newton added orange and indigo to make seven colors in the rainbow. He was enamored of the Pythagorean idea of a “harmony of the universe” (musica universalis) and thought the rainbow ought to reflect the pitches of the musical scale, as well as the known objects in the solar system at the time and even the days of the week.
Never mind that the scale and the week are also arbitrary and the astronomical count turned out incorrect — it’s a thing we do, grabbing on to patterns and relationships to make sense of things. But the divisions themselves are neither right nor wrong — just useful.
More on the pitch/color connection:
The man who heard his paintbox hiss (the synaesthesia of Kandinsky)
Music for Measure: on the 300th Anniversary of Newton’s ‘Opticks’
Follow Dale on Facebook:
Overtones: Every note is a chord
Listen to this:
That’s a low C, a single note played on a piano. At least that’s how I’d have described it when I was 13. Within a year I was hearing that very differently, thanks to two great musicians.
One was my older brother Ron, who started playing piano when he was seven and I was three. I grew up in his shadow, musically and literally, laying by his feet while he played Chopin and Ravel, Scott Joplin and West Side Story (which he can still shred). He led me to Elton John and Genesis (until Genesis betrayed all that was good) and Jesus Christ Superstar. When I said The Rite of Spring was just noise, he ordered me to put the headphones on and listen again. And then I couldn’t stop.
When I was 14, Ron introduced me to my second huge musical influence by bringing home a set of LPs from the library. It wasn’t music, but a lecture series about music: Leonard Bernstein’s 1973 Norton Lectures at Harvard.
What Carl Sagan did for me with science, Bernstein did with music. I’d never heard anybody talk about music like Bernstein did in those lectures. He went below the surface in a way that was completely new to me. It was the start of my interest in music theory, which turned into a major, my first career, and a lifelong fascination.
The topic Bernstein covers first is the most stunning of all — that a single pitch contains an infinite number of pitches.
This isn’t an abstraction. These other pitches are tangible, and that matters. It’s one of the hidden keys to the ability of music to communicate emotions. But for reasons I’ve never understood, most of the current top-selling music theory textbooks never talk about it at all.
Actually, I do know why they leave it out: it isn’t necessary. It’s merely wonderful.
Don’t Skip the Miracle
Sound results from vibrations. The more regular the vibrating body is in structure — tuning fork, metal string, column of air — the less like noise the sound will be, and the more distinctively “pitched” and musical it sounds. The faster the vibration, the higher the pitch. As you go from left to right on the piano keyboard, you go from low to high, the strings get shorter and therefore vibrate faster, and the pitch gets higher.
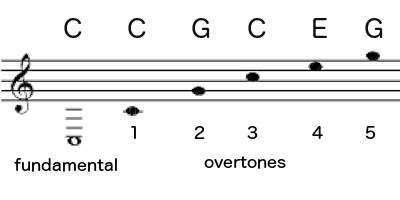
The low C at the top of the post resulted when a felt hammer hit a string of a certain length in my piano. The string vibrated about 100 times a second (100 Hertz, or 100 Hz) along its entire length to produce that pitch.
If you double the speed of vibration to 200 Hz, the pitch goes up one octave to the next higher C. A string half as long will do this.
To go up another octave to the next C, just double the vibration again to 400 times a second. A string a fourth as long as the original one will vibrate four times faster, and you’ve got the next C.
And on it goes, with Cs at 800, 1600, 3200. You can hear the family resemblance between notes that are an octave apart. They’re like higher and lower versions of each other because of this simple ratio. If men and boys sing the same melody at the same time, they will tend to be an octave apart. But it doesn’t sound like they’re singing two different parts — just the same melody doubled at the octave. That’s how close the family resemblance is.
Play the low C again.
That string is vibrating at about 100 Hz along its entire length to produce the pitch C. Here’s a schematic of the string in vibration along its entire length:
Now here’s where it gets strange: at the same time it’s vibrating along its full length, the two halves of that string are vibrating independently. And because they’re half as long, they’re going twice as fast (200 Hz). Don’t ask me how this works — magic, I assume. We know that doubling the vibration sends the pitch up an octave. So in addition to the low C, you are also hearing the C an octave higher at the same time.
Again, I’m not saying you are “hearing it,” in quotes, like it’s some hypothetical thing. When you play a low C, you are also actually hearing the C an octave higher. It’s a small but audible fraction of the sound. The note you’re playing is called the fundamental. The higher C is the first overtone. But because the two Cs have such a strong family resemblance, it’s hard to hear it. They are too similar.
Fortunately the string is also vibrating in thirds, at 300 Hz. That produces a G, the second overtone, which is usually pretty clear. Here’s the pitch for G, so you can get it in your ear:
The string is also vibrating in fourths (400 Hz), which is four times as fast as the low C and twice as fast as the second C, so that produces yet another C, an octave higher still:
And also in fifths (500 Hz), which produces an E. This one will be fainter, but because it’s not another C, you can usually hear it. Here’s the pitch to listen for:
And also in sixths (600 Hz), which is twice as fast as the G, so that’s another, higher G:
The divisions of the string continue infinitely in smaller and smaller intervals, all vibrating simultaneously and producing an infinite number of pitches. But after about the fifth overtone, the vibrations are such a tiny sliver of the sound that you usually can’t hear them.
No worries, we’ve already achieved the magic. When you play a C, you actually hear all of these pitches:
I don’t mean to startle you, but that’s a C major chord. When you play a C, you don’t just hear a C, you hear the pitches of a C major chord — C, E, and G. It’s not only C that does this, of course — play any pitch, and you are actually hearing not just that pitch, but a major chord based on that pitch. It’s more subtle than that recording, but you can hear it, and we will shortly.
We could do the same with any pitch: A, F#, Bb, anything. Because of the physics of vibration, each of them produces its own major chord.
Why do overtones matter? Because the emotional fuel of music is the interaction between pitches sounding simultaneously — harmony. And when you play any two pitches, it isn’t just those two pitches interacting – there’s a whole cloud of other notes above them interacting as well. (More on this when we get to consonance and dissonance.)
Now it’s time to hear the overtones, not as bells outlined on my synthesizer, but coming out of an actual single pitch. Turn the volume up a little. A lot of things affect how strongly overtones pop out when you play a note, including humidity and whether the piano is in tune. My piano is not, but the day was humid, so we’ll see what happens. I’ll play that low C one more time, and you listen for the second and fourth overtones (G and E) blooming out of the sound:
Oh man, this was a good day for overtones. The G blooms out almost immediately. The E and the next G become audible around 4 seconds. And right around 5 seconds…
Oh my. (Whispery teacher voice.) Boys and girls, we have a very special guest today. Around the 5-second mark, you begin to hear an overtone that is usually not audible — the sixth overtone, which results from the string vibrating in sevenths. This one’s an oddball to Western ears because it doesn’t correspond to an actual pitch we use. It lands in the crack between A and B-flat on the piano. But there it is, ringing out all the way to the end like it has no shame:
(Now go back and play the C again. Did you hear the B-extra-flat, especially after the others have died out a bit? It can help if you whistle or hum the pitch you’re looking for.)
Don’t be sad and scared if you can’t hear the overtones right away. You will eventually, and once you do, you’ll get quicker at it. It’s like those Magic Eye stereograms from the 90s where you [tippy title=”make your eyes go wonky”]Start with the image an inch from your nose. Gradually pull it back without adjusting your eyes.[/tippy] and boom, you see a space shuttle or the Mona Lisa or whatever:
Your assignment: Get to an actual piano. Thump that low C and hold it down. As the fundamental pitch decays, the overtones will bloom out of the sound, especially the G and E. If you’re lucky, you’ll even spot the exotic B-extra-flat.
Extra credit: Nine minutes of Leonard Bernstein demonstrating the same thing in a slightly different way. These are from the actual Harvard lectures I heard on LPs at 14.
[arve url=”https://www.youtube.com/watch?v=8n3qMB6AD_0″ /]
[arve url=”https://www.youtube.com/watch?v=iDTj6tBnHlA” /]
Can you hear the overtones? Tell me in the comments.
(Next post: Pitch.)
Click LIKE below to follow Dale McGowan on Facebook!