Overtones: Every note is a chord
Listen to this:
That’s a low C, a single note played on a piano. At least that’s how I’d have described it when I was 13. Within a year I was hearing that very differently, thanks to two great musicians.
One was my older brother Ron, who started playing piano when he was seven and I was three. I grew up in his shadow, musically and literally, laying by his feet while he played Chopin and Ravel, Scott Joplin and West Side Story (which he can still shred). He led me to Elton John and Genesis (until Genesis betrayed all that was good) and Jesus Christ Superstar. When I said The Rite of Spring was just noise, he ordered me to put the headphones on and listen again. And then I couldn’t stop.
When I was 14, Ron introduced me to my second huge musical influence by bringing home a set of LPs from the library. It wasn’t music, but a lecture series about music: Leonard Bernstein’s 1973 Norton Lectures at Harvard.
What Carl Sagan did for me with science, Bernstein did with music. I’d never heard anybody talk about music like Bernstein did in those lectures. He went below the surface in a way that was completely new to me. It was the start of my interest in music theory, which turned into a major, my first career, and a lifelong fascination.
The topic Bernstein covers first is the most stunning of all — that a single pitch contains an infinite number of pitches.
This isn’t an abstraction. These other pitches are tangible, and that matters. It’s one of the hidden keys to the ability of music to communicate emotions. But for reasons I’ve never understood, most of the current top-selling music theory textbooks never talk about it at all.
Actually, I do know why they leave it out: it isn’t necessary. It’s merely wonderful.
Don’t Skip the Miracle
Sound results from vibrations. The more regular the vibrating body is in structure — tuning fork, metal string, column of air — the less like noise the sound will be, and the more distinctively “pitched” and musical it sounds. The faster the vibration, the higher the pitch. As you go from left to right on the piano keyboard, you go from low to high, the strings get shorter and therefore vibrate faster, and the pitch gets higher.
The low C at the top of the post resulted when a felt hammer hit a string of a certain length in my piano. The string vibrated about 100 times a second (100 Hertz, or 100 Hz) along its entire length to produce that pitch.
If you double the speed of vibration to 200 Hz, the pitch goes up one octave to the next higher C. A string half as long will do this.
To go up another octave to the next C, just double the vibration again to 400 times a second. A string a fourth as long as the original one will vibrate four times faster, and you’ve got the next C.
And on it goes, with Cs at 800, 1600, 3200. You can hear the family resemblance between notes that are an octave apart. They’re like higher and lower versions of each other because of this simple ratio. If men and boys sing the same melody at the same time, they will tend to be an octave apart. But it doesn’t sound like they’re singing two different parts — just the same melody doubled at the octave. That’s how close the family resemblance is.
Play the low C again.
That string is vibrating at about 100 Hz along its entire length to produce the pitch C. Here’s a schematic of the string in vibration along its entire length:
Now here’s where it gets strange: at the same time it’s vibrating along its full length, the two halves of that string are vibrating independently. And because they’re half as long, they’re going twice as fast (200 Hz). Don’t ask me how this works — magic, I assume. We know that doubling the vibration sends the pitch up an octave. So in addition to the low C, you are also hearing the C an octave higher at the same time.
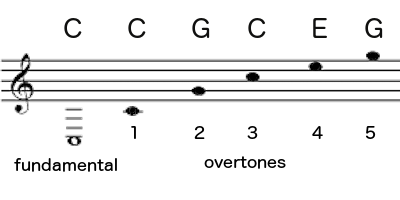
Again, I’m not saying you are “hearing it,” in quotes, like it’s some hypothetical thing. When you play a low C, you are also actually hearing the C an octave higher. It’s a small but audible fraction of the sound. The note you’re playing is called the fundamental. The higher C is the first overtone. But because the two Cs have such a strong family resemblance, it’s hard to hear it. They are too similar.
Fortunately the string is also vibrating in thirds, at 300 Hz. That produces a G, the second overtone, which is usually pretty clear. Here’s the pitch for G, so you can get it in your ear:
The string is also vibrating in fourths (400 Hz), which is four times as fast as the low C and twice as fast as the second C, so that produces yet another C, an octave higher still:
And also in fifths (500 Hz), which produces an E. This one will be fainter, but because it’s not another C, you can usually hear it. Here’s the pitch to listen for:
And also in sixths (600 Hz), which is twice as fast as the G, so that’s another, higher G:
The divisions of the string continue infinitely in smaller and smaller intervals, all vibrating simultaneously and producing an infinite number of pitches. But after about the fifth overtone, the vibrations are such a tiny sliver of the sound that you usually can’t hear them.
No worries, we’ve already achieved the magic. When you play a C, you actually hear all of these pitches:
I don’t mean to startle you, but that’s a C major chord. When you play a C, you don’t just hear a C, you hear the pitches of a C major chord — C, E, and G. It’s not only C that does this, of course — play any pitch, and you are actually hearing not just that pitch, but a major chord based on that pitch. It’s more subtle than that recording, but you can hear it, and we will shortly.
We could do the same with any pitch: A, F#, Bb, anything. Because of the physics of vibration, each of them produces its own major chord.
Why do overtones matter? Because the emotional fuel of music is the interaction between pitches sounding simultaneously — harmony. And when you play any two pitches, it isn’t just those two pitches interacting – there’s a whole cloud of other notes above them interacting as well. (More on this when we get to consonance and dissonance.)
Now it’s time to hear the overtones, not as bells outlined on my synthesizer, but coming out of an actual single pitch. Turn the volume up a little. A lot of things affect how strongly overtones pop out when you play a note, including humidity and whether the piano is in tune. My piano is not, but the day was humid, so we’ll see what happens. I’ll play that low C one more time, and you listen for the second and fourth overtones (G and E) blooming out of the sound:
Oh man, this was a good day for overtones. The G blooms out almost immediately. The E and the next G become audible around 4 seconds. And right around 5 seconds…
Oh my. (Whispery teacher voice.) Boys and girls, we have a very special guest today. Around the 5-second mark, you begin to hear an overtone that is usually not audible — the sixth overtone, which results from the string vibrating in sevenths. This one’s an oddball to Western ears because it doesn’t correspond to an actual pitch we use. It lands in the crack between A and B-flat on the piano. But there it is, ringing out all the way to the end like it has no shame:
(Now go back and play the C again. Did you hear the B-extra-flat, especially after the others have died out a bit? It can help if you whistle or hum the pitch you’re looking for.)
Don’t be sad and scared if you can’t hear the overtones right away. You will eventually, and once you do, you’ll get quicker at it. It’s like those Magic Eye stereograms from the 90s where you [tippy title=”make your eyes go wonky”]Start with the image an inch from your nose. Gradually pull it back without adjusting your eyes.[/tippy] and boom, you see a space shuttle or the Mona Lisa or whatever:
Your assignment: Get to an actual piano. Thump that low C and hold it down. As the fundamental pitch decays, the overtones will bloom out of the sound, especially the G and E. If you’re lucky, you’ll even spot the exotic B-extra-flat.
Extra credit: Nine minutes of Leonard Bernstein demonstrating the same thing in a slightly different way. These are from the actual Harvard lectures I heard on LPs at 14.
[arve url=”https://www.youtube.com/watch?v=8n3qMB6AD_0″ /]
[arve url=”https://www.youtube.com/watch?v=iDTj6tBnHlA” /]
Can you hear the overtones? Tell me in the comments.
(Next post: Pitch.)
Click LIKE below to follow Dale McGowan on Facebook!