Scales! Wait. Come back.
I hated scales in middle school. Oh I was good at scales, even got a certificate for playing all four forms of every scale by memory on my wee clarinet. I was a good boy.
And still I hated them.
It just seemed like such a pointless, hoop-jumping thing to me. Memorize these note patterns, then play each one starting from every possible note, and you win. But aside from the value of rote memorization and the fingering practice…what was the point?
There were other unanswered questions in my head — like Why are there three different kinds of minor scales? Why is the melodic minor different going up and going down? Why does the harmonic minor make me sound like a snake charmer? Why does minor sound sad and major sound happy? Are these the only four ways to get from C to C?
It’s like the Steven Wright joke
Why is the alphabet in that order? Is it because of that song?
Scales are actually cool and interesting once you know what they’re for. Stick with me to the end of the post, then tell me if I’m wrong. (Spoiler: I’m not.)
Last time I split the octave into 12 equal parts to make the chromatic scale. The name hints at the purpose. By containing all 12 of the pitches we use in Western music, the chromatic scale is like a paint store with 12 available colors.
You don’t want every available color for a painting project. You choose a palette — a subset of colors, a theme. If you want this result:
…don’t use every color in the store. Use this palette:
Same for music. The chromatic scale has every available pitch in the Western tonal system. The distance from one to the next is a half step. Here are the 12 half steps of the chromatic scale (plus the next C):
When I write a piece, I don’t need every note. If I want a certain mood, I’ll choose a subset of pitches from the 12 available, and a different subset gets me a different mood.
Example: If I choose every other pitch, instead of 12 notes a half step apart, I’ll have 6 notes a whole step apart. That’s called a whole tone scale:
There’s something strange about that scale, right? It starts going off the rails at the 4th note and never gets normal again. Here’s why: All of the pitches are the same distance apart. No half steps. Because of that, your ear can’t easily track where you are. Aside from whatever note we happen to start on, none of the pitches stands out as “home,” so the whole tone scale creates music with an ethereal, directionless quality. If you were a child of the 70s, you know it well. Whenever there was a campy flashback in The Brady Bunch, or Scooby Doo was being hypnotized, there’s a good chance a harp or bells were playing music drawn from a whole tone scale:
One particular Debussy piano piece called Voiles (Sails) is the go-to for illustrating a whole tone scale. Feel that unanchored, homeless quality (0:47):
[arve url=”https://www.youtube.com/watch?v=95_OvaRHwDg” parameters=”start=9 end=56″ /]
The fact that pretty much every theory teacher uses sitcom flashbacks and one Debussy piece as whole tone examples shows you just how rare it is. Beyond drifty sails and coming unstuck in time, a scale with all the pitches equally spaced just isn’t all that useful. If someone gave you driving directions like this — Go one block and left, one block and right, one block and right, one block and left, one block and right, and on and on across town, you’d have a helluva time finding your way home again. Every step is the same. It’s confusing.
If instead the directions were Go one block and left, three blocks and right, one block and left, then five blocks and you’re there — now the steps are different enough to landmark in your head. You need a scale that works the same way — a mix of steps of different sizes so your ear knows where you are relative to home.
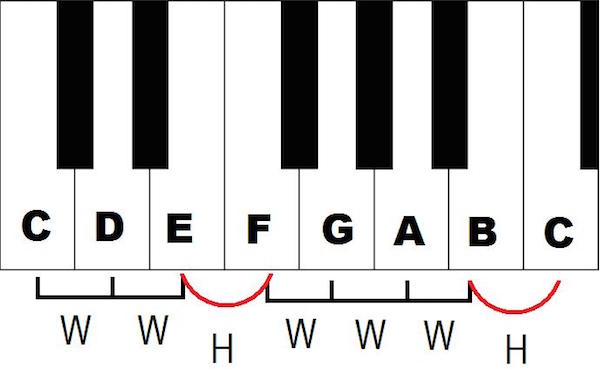
Major and minor scales do just that, creating a pattern of pitches that are different distances apart. They do it by choosing only 7 of the 12 notes, leaving gaps where the other pitches were. The scale shows the ladder of steps between the notes if you arrange them in order. Here’s a C major scale:
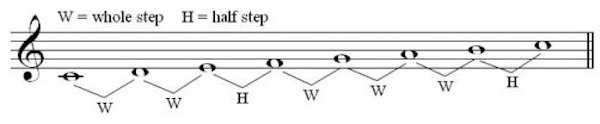
You start on C but leave out C# and go to D — a whole step. It’s like going from red to orange and skipping reddish-orange. The major scale then goes another whole step (to E), then a half step (F), then three more whole steps (G-A-B), and finally a half step to the next C. If you start on C, the white keys on a piano fall naturally into the major scale without any adjustments. The black keys are the gaps, the five chromatic pitches that were left out of the major scale:
If you start on a note other than C, you’ll have to raise or lower notes along the way, using flats and sharps on the page and black keys on the piano to get the same pattern of whole steps and half steps.
Scales aren’t meant to be played in that order any more than the letters in a word are supposed to be spelled out in alphabetical order, or a set of colors in your paint theme is supposed to be painted left to right on the wall by wavelength. Hey, rainbows are great, but you don’t want a rainbow every time you paint. So when you paint your house, this is the scale:
…and this is the music:
The scale is a set of instructions to pick out the colors (pitches) that establish a certain palette (key) for the music you want to write.
But music goes beyond the visual analogy to something that makes its emotional power possible. This pattern also creates a kind of aural map. The sequence of half and whole steps sticks a pin in one of the notes, calling it home, then creates a series of landmarks to tell you where you are relative to that home at all times. By listening to music all your life, your ear has learned how to follow that map — to go away from home, have adventures, and return (or not). The next three JET posts will get into that.
The minor scale is a different pattern of whole steps and half steps spanning the octave. The result is a different emotional palette:
The minor scale results when you lower the third, sixth, and seventh pitches of the major. That’s worth remembering. No need to memorizing key signatures or build scales yourself, but we’ll certainly talk about the various shenanigans the third, sixth, and seventh notes of the scale get up to.
Three great scales from elsewhere
Step outside of Western music and you can really start to see how different scales color the music. I hinted at that last time with the Carnatic microtonal scales. (Don’t be skipping stuff, or all is lost.) Here are three more.
Arabic music has at least 90 different scales, or maqam, each of which provides a different mood. Here’s one, maqam nawa athar:
Which sounds like this:
Hear that? It’s just crammed with intervals that sound exotic to Western ears. If a major scale is a map across your hometown, this one is a map to the market in Marrakech.
Several of the pitches of the Indonesian pelog scale fall in the gaps between our notes, which further shows that all scale divisions are arbitrary and cultural. You can’t even notate pelog properly with Western notation. If you try, you end up with these apologetic little plus and minus signs to indicate “a little higher” or “a little lower” than the notation:
And why not? Remember the sixth overtone, the B-extra-flat? To Western listeners, these pitches sound out of tune because they don’t match our particular divisions, but they have no less claim. Here’s pelog:
And here’s a phenomenal Balinese gamelan playing music using a variant of pelog. If you haven’t heard Balinese gamelan before, strap in, this is awesome:
[arve url=”https://www.youtube.com/watch?v=ldPMifPbngc” /]
Want to evoke a Middle Eastern vibe? Use the Byzantine scale:
It starts with a half step, which is instantly exotic (neither major nor minor does that), and twice again you get that wide step and a half (the ties above). The composer Saint-Saëns knew he could throw you into the ancient Levant for his opera Samson and Delilah by using the Byzantine scale:
[arve url=”https://www.youtube.com/watch?v=TEhor3HeulE” parameters=”start=9 end=34″ /]
Other minors and the modes down the road. Now go outside and play.
Overtones: Every note is a chord
Listen to this:
That’s a low C, a single note played on a piano. At least that’s how I’d have described it when I was 13. Within a year I was hearing that very differently, thanks to two great musicians.
One was my older brother Ron, who started playing piano when he was seven and I was three. I grew up in his shadow, musically and literally, laying by his feet while he played Chopin and Ravel, Scott Joplin and West Side Story (which he can still shred). He led me to Elton John and Genesis (until Genesis betrayed all that was good) and Jesus Christ Superstar. When I said The Rite of Spring was just noise, he ordered me to put the headphones on and listen again. And then I couldn’t stop.
When I was 14, Ron introduced me to my second huge musical influence by bringing home a set of LPs from the library. It wasn’t music, but a lecture series about music: Leonard Bernstein’s 1973 Norton Lectures at Harvard.
What Carl Sagan did for me with science, Bernstein did with music. I’d never heard anybody talk about music like Bernstein did in those lectures. He went below the surface in a way that was completely new to me. It was the start of my interest in music theory, which turned into a major, my first career, and a lifelong fascination.
The topic Bernstein covers first is the most stunning of all — that a single pitch contains an infinite number of pitches.
This isn’t an abstraction. These other pitches are tangible, and that matters. It’s one of the hidden keys to the ability of music to communicate emotions. But for reasons I’ve never understood, most of the current top-selling music theory textbooks never talk about it at all.
Actually, I do know why they leave it out: it isn’t necessary. It’s merely wonderful.
Don’t Skip the Miracle
Sound results from vibrations. The more regular the vibrating body is in structure — tuning fork, metal string, column of air — the less like noise the sound will be, and the more distinctively “pitched” and musical it sounds. The faster the vibration, the higher the pitch. As you go from left to right on the piano keyboard, you go from low to high, the strings get shorter and therefore vibrate faster, and the pitch gets higher.
The low C at the top of the post resulted when a felt hammer hit a string of a certain length in my piano. The string vibrated about 100 times a second (100 Hertz, or 100 Hz) along its entire length to produce that pitch.
If you double the speed of vibration to 200 Hz, the pitch goes up one octave to the next higher C. A string half as long will do this.
To go up another octave to the next C, just double the vibration again to 400 times a second. A string a fourth as long as the original one will vibrate four times faster, and you’ve got the next C.
And on it goes, with Cs at 800, 1600, 3200. You can hear the family resemblance between notes that are an octave apart. They’re like higher and lower versions of each other because of this simple ratio. If men and boys sing the same melody at the same time, they will tend to be an octave apart. But it doesn’t sound like they’re singing two different parts — just the same melody doubled at the octave. That’s how close the family resemblance is.
Play the low C again.
That string is vibrating at about 100 Hz along its entire length to produce the pitch C. Here’s a schematic of the string in vibration along its entire length:
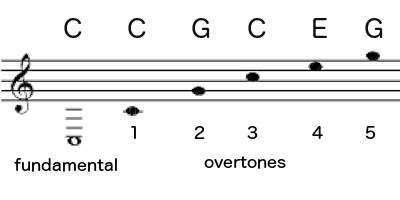
Now here’s where it gets strange: at the same time it’s vibrating along its full length, the two halves of that string are vibrating independently. And because they’re half as long, they’re going twice as fast (200 Hz). Don’t ask me how this works — magic, I assume. We know that doubling the vibration sends the pitch up an octave. So in addition to the low C, you are also hearing the C an octave higher at the same time.
String vibrating in halves
Again, I’m not saying you are “hearing it,” in quotes, like it’s some hypothetical thing. When you play a low C, you are also actually hearing the C an octave higher. It’s a small but audible fraction of the sound. The note you’re playing is called the fundamental. The higher C is the first overtone. But because the two Cs have such a strong family resemblance, it’s hard to hear it. They are too similar.
Fortunately the string is also vibrating in thirds, at 300 Hz. That produces a G, the second overtone, which is usually pretty clear. Here’s the pitch for G, so you can get it in your ear:
String vibrating in thirds
The string is also vibrating in fourths (400 Hz), which is four times as fast as the low C and twice as fast as the second C, so that produces yet another C, an octave higher still:
And also in fifths (500 Hz), which produces an E. This one will be fainter, but because it’s not another C, you can usually hear it. Here’s the pitch to listen for:
And also in sixths (600 Hz), which is twice as fast as the G, so that’s another, higher G:
The divisions of the string continue infinitely in smaller and smaller intervals, all vibrating simultaneously and producing an infinite number of pitches. But after about the fifth overtone, the vibrations are such a tiny sliver of the sound that you usually can’t hear them.
No worries, we’ve already achieved the magic. When you play a C, you actually hear all of these pitches:
I don’t mean to startle you, but that’s a C major chord. When you play a C, you don’t just hear a C, you hear the pitches of a C major chord — C, E, and G. It’s not only C that does this, of course — play any pitch, and you are actually hearing not just that pitch, but a major chord based on that pitch. It’s more subtle than that recording, but you can hear it, and we will shortly.
We could do the same with any pitch: A, F#, Bb, anything. Because of the physics of vibration, each of them produces its own major chord.
Why do overtones matter? Because the emotional fuel of music is the interaction between pitches sounding simultaneously — harmony. And when you play any two pitches, it isn’t just those two pitches interacting – there’s a whole cloud of other notes above them interacting as well. (More on this when we get to consonance and dissonance.)
Now it’s time to hear the overtones, not as bells outlined on my synthesizer, but coming out of an actual single pitch. Turn the volume up a little. A lot of things affect how strongly overtones pop out when you play a note, including humidity and whether the piano is in tune. My piano is not, but the day was humid, so we’ll see what happens. I’ll play that low C one more time, and you listen for the second and fourth overtones (G and E) blooming out of the sound:
Oh man, this was a good day for overtones. The G blooms out almost immediately. The E and the next G become audible around 4 seconds. And right around 5 seconds…
Oh my. (Whispery teacher voice.) Boys and girls, we have a very special guest today. Around the 5-second mark, you begin to hear an overtone that is usually not audible — the sixth overtone, which results from the string vibrating in sevenths. This one’s an oddball to Western ears because it doesn’t correspond to an actual pitch we use. It lands in the crack between A and B-flat on the piano. But there it is, ringing out all the way to the end like it has no shame:
(Now go back and play the C again. Did you hear the B-extra-flat, especially after the others have died out a bit? It can help if you whistle or hum the pitch you’re looking for.)
Don’t be sad and scared if you can’t hear the overtones right away. You will eventually, and once you do, you’ll get quicker at it. It’s like those Magic Eye stereograms from the 90s where you [tippy title=”make your eyes go wonky”]Start with the image an inch from your nose. Gradually pull it back without adjusting your eyes.[/tippy] and boom, you see a space shuttle or the Mona Lisa or whatever:
See it?
Your assignment: Get to an actual piano. Thump that low C and hold it down. As the fundamental pitch decays, the overtones will bloom out of the sound, especially the G and E. If you’re lucky, you’ll even spot the exotic B-extra-flat.
Extra credit: Nine minutes of Leonard Bernstein demonstrating the same thing in a slightly different way. These are from the actual Harvard lectures I heard on LPs at 14.
[arve url=”https://www.youtube.com/watch?v=8n3qMB6AD_0″ /]
[arve url=”https://www.youtube.com/watch?v=iDTj6tBnHlA” /]
Can you hear the overtones? Tell me in the comments.
(Next post: Pitch.)
Click LIKE below to follow Dale McGowan on Facebook!
The Music That Broke My Heart
- September 01, 2015
- By Dale McGowan
- In Intro
1
During the weeks of shock and grief after the attacks of September 11, 2001, one piece of music was added to the programs of over 50 American symphony orchestras: Samuel Barber’s Adagio for Strings.
Vedran Smailović, “Cellist of Sarajevo,” in the ruins of the National Library, 1992
This piece was already special to me. When I first heard it at 18, I cried uncontrollably. It wasn’t just generally “sad” for me — it seemed to bring out the exact sequence of emotions I’d felt after the death of my dad five years earlier. I felt my grief unfolding in a painfully familiar way.
What the hell? There were no evocative lyrics, no title like “Death of a Dad” to prime my emotional pump — just pitches arranged over time, played by a string orchestra.
Five years later, after studying music theory in college, I sat down with the Adagio to figure out how Barber had communicated grief so effectively.
After a few minutes with the score, I saw what he’d done. It was brilliant, something anyone could understand if they just had a little [tippy title=”music theory”]The study of the grammar, syntax, and semantics of music.[/tippy]. Just a little music theory is all you need to unlock this emotional language and know how music works. Of course the great thing is that it works even if you don’t know how it does.
But oh, the knowing.
When the Adagio was added to the programs of all those orchestras after 9/11, NPR invited a “cultural commentator” to explain what it was about that particular piece that captured grief so well for so many people. Given his answer, he should have said, “Beats me.” Instead, he said roughly this:
When President Roosevelt died in 1945, the funeral planners went looking for appropriate music for his service. They knew they wanted something slow and beautiful. Barber’s Adagio, which was written just a few years earlier, was slow and beautiful, and it was selected for the funeral. Eighteen years later, the piece was played again for the funeral of JFK, in part because it had been in FDR’s funeral. From that point forward, Barber’s Adagio became associated with sadness in the national mind.
I was slack-jawed. He flipped the cause and effect. It’s like saying the 23rd Psalm is comforting because it’s been used to comfort people for so long. It’s like saying Tabasco sauce is considered hot because it’s in Cajun food.
Neither psalm nor sauce nor Adagio became what it is by association alone. In each case, most of what hits us is in the thing itself.
Tragedy, desperation, false hope, and exhausted resignation are all woven into the music of the Adagio, which then reaches me because my brain recognizes the emotional language in which it’s written. I knew how Barber had done it. But NPR never called, so I explained it to my dog.
He was impressed.
Eight years later, conductor and composer Rob Kapilow was talking about the Adagio on NPR for the Barber centennial. He said the kind of catharsis the piece goes through is similar to the catharsis at a funeral:
It starts from incredible sadness, builds to an incredible climax of intensity, and then finally reaches a kind of serene acceptance, which is completely appropriate for those occasions.
That’s good stuff. He’s talking funerals again, but he’s not saying funerals caused the music to sound sad. He’s saying the music parallels the emotional process in grief, which it does. Now he’ll talk about what makes the sadness, and what underpins that climax — the [tippy title=”harmony”]The relationship of pitches sounding at the same time.[/tippy].
It starts off with just a single note. And it’s so pure, it’s as if that note somehow was there forever.
That’s neat. Now talk about the harmony.
So Barber lets you sit there, with that one note on the violin, for an incredibly long time, and then the note gets drenched with the emotion of a rich chord in the strings. Finally it has to move, and it starts this lovely first phrase, which seems to take forever.
Yes, there is much foreverness. Now talk about the harmony. He knows what that “rich chord” is, of course — Kapilow’s an Eastman-trained composer. He just doesn’t think he can explain it to the layperson within the limits of a radio program. But this is NPR, dammit. That’s what they do.
He doesn’t have to say it’s a subdominant minor-minor seventh chord. But he can say this: Because of the grammar of music you’ve grown up hearing, the first two chords create an arrow of harmony that points your ears to a very specific place you don’t want to go. Then the next two chords suddenly lift you out of danger like a helicopter taking you off the roof.
Then you play those 30 seconds, and you can feel it happening.
In the next 30 seconds, after a moment of relief, you feel yourself sinking back to where we started — the same two chords, that harmonic arrow to despair. The escape didn’t work. Silence — then you try again.
But he doesn’t talk about harmony (notes played simultaneously). He talks about melody (notes played in sequence):
You have a sequence of three notes up, three notes up again, then you do it up a step. Then you do it again. And then … just, stop. The simplest pattern. A whole second wing of copying the pattern starts in the violas. Gradually, the slow repetitions acquire more expression and emotion. The piece gets higher and fuller.
It’s all true. The three-note, repeating-and-rising thing is very nice. But talking about the three-note melodic pattern as if it’s The Thing is like explaining the effectiveness of the “I Have a Dream” speech by describing Martin Luther King’s hand gestures. That’s part of what made the speech work, I suppose, but you can’t talk about why that speech became the iconic King speech without looking at the content, and the meaning that content conveyed.
In language, the primary (though not exclusive) vehicle of meaning is words and sentences. In [tippy title=”music”](i.e. Western tonal music).[/tippy], the primary vehicle of meaning is chords and chord progressions — the harmony.
He continues:
The simplicity of the logic is to make you feel the universality of the journey: from the simple note to the high emotional wailing to release and to final acceptance, but never in the place you thought it was going to lead you to.
Oo! That last bit was good. And what was that unexpected place? Not an unexpected three-note pattern. Not a sudden naked bagpipe solo. It takes you somewhere that’s harmonically unexpected. And if you (like me) were raised hearing the syntax and semantics of Western music, then Barber is speaking your language, and you feel it.
Yes, you need to know music theory to understand the harmonic language of music. But here’s the thing: you don’t need a lot of theory. You need just enough theory to unlock what’s going on. Maybe that’s still too much for a five-minute radio piece to get into, but a blog stretches to the horizon. We can even go beyond the theory to the fascinating intersection of physics, biology, culture, and personal experience that makes the emotional language of music comprehensible for one person or group but not another. So here we are, with you deciding whether to keep reading.
Keep reading.
If you’re willing to put in the effort to learn just enough theory, I’d love to share it. The basics will take about 12 posts, and I’ll scatter a lot of music in there as well. Then once we’ve covered the basics, we can talk about music in a whole new way, which is what the blog will do forever. For reference, the original teaching posts will always be in the right sidebar under the heading Just Enough Theory. I’ve also added a hover feature so you can get the definitions of a few key terms in any post. [tippy title=”Hover over any text with a blue dotted underline, like this…”]…and a quick definition or comment will pop up.[/tippy]
At some point, I’ll circle back and talk about the Adagio in great detail, but not for a while. First we’ll apply music theory to a lot of other music, especially music you suggest. To allow time for conversation in the comments, posts will be weekly for a while, then I’ll pick up the pace.
To play us out, here’s Leonard Slatkin and the St. Louis Symphony with the piece that made me want to know how music does that.
[arve url=”https://www.youtube.com/watch?v=wBK30bJagEA” /]
Click LIKE below to follow Dale McGowan on Facebook!
Photo of Vedran Smailović by Mikhail Evstafiev. Licensed under CC BY-SA 3.0 via Commons.
