Consonance is Nice. Dissonance is Delicious.
15 min
This is Your Brain on Music is a really good book about the neuroscience of music. There are about 4,000 good sentences in it. So it might seem petty to talk about the one sentence that made me sad, but that’s how sad it made me:
Musicians refer to pleasing-sounding chords and intervals as consonant and the unpleasing ones as dissonant.
Be a love: Take a Brillo pad and scrub that sentence from your monitor. If you have the book at home, scrub it out there as well. Page 62. I’ll wait.
[…]
By the end of this post, I hope you’ll see how tragically wrongheaded it is to call dissonance “unpleasing”. The really effective, moving moments in music almost always include dissonance, sometimes a lot of it, just as the really effective rollercoasters almost always include hills. These aren’t bugs–they are features.
I mean gah.
A flat rollercoaster and dissonance-free music are so off-point that they are given completely new names, like “light rail” and “Enya.” Good for getting you massaged and moving you from place to place, maybe, but not for moving you. The interplay of dissonance and consonance, tension and release, is one of the ingredients that makes Western music work. It’s a sliding scale defined by more or less complexity in the relationship of pitches.
Pitch combinations aren’t just “consonant” or “dissonant” — like everything we seem to talk about here, there’s a spectrum. So please keep your arms inside the car as we head into that spectrum.
Some Quick Terms
The distance between two pitches is an interval. If it’s one note following another like a melody, it’s a melodic interval. Two notes at the same time is a harmonic interval. That’s where the real emotional juice is.
Intervals are named by the distance between the notes. From any note up to the very next note name is called a second. Skip one and it’s a third. Skip two names and it’s a fourth, and so on. So in the scale below…
…C→D, E→F, and A→B are all seconds. C→E is a third. C→F is a fourth. C→A is a sixth.
What about flats and sharps? C→D♭ is still called a second because it’s going from one pitch name to the next. But it’s a minor second (or half step), the Jaws interval, duh-dump. C→D is a major second (or whole step), the Chopsticks interval, which is less dissonant than the minor (depending on the child and the piano, I guess). And C to G♭ is still a fifth, but a diminished fifth, a.k.a. a tritone, a.k.a. “the devil in music,” about which more below.
If this were my theory class, we’d now drill intervals for two weeks. You’d learn how to identify and spell minor, major, perfect, augmented, and diminished intervals starting on every pitch. You’d bite back your tears, determined to meet the interval on its own terms, driven by grudging respect for my lunatic quest for perfection.
[arve url=”https://www.youtube.com/watch?v=VnuImW1dWAk” parameters=”start=87 end=103″ /]
But we’re doing Just Enough Theory here, so we’ll skim lightly over the cool surface, emphasizing dissonance, with the Devil as our special guest.
Consonance and Dissonance
The technical explanation of consonance and dissonance is the ratio of vibrations of the two pitches.
The ultimate consonance is a unison. It’s not harmony — just one note playing with itself, which is sinful. The ratio is 1:1. Add another pitch and you get intervals.
Octaves, fifths, fourths, and thirds are very consonant. They sound like this:
Simple vibration ratios are consonant, in part because there’s a lot of matching and little close conflict in their overtones. The [tippy title=”octave”](‘Some-where’ [over the rainbow])[/tippy] is the most consonant (besides the unison). The top note vibrates twice as fast as the bottom, a simple ratio of 1:2. A fifth is a ratio of 2:3, and a fourth is 3:4, etc.
That’s the technical explanation. But the most important thing is that you can hear it. Here’s some [tippy title=”real consonance at work”]Aaron Copland, Fanfare for the Common Man[/tippy]:
[arve url=”https://www.youtube.com/embed/4NjssV8UuVA” parameters=”start=22 end=52″ /]
Hear how open, relaxed, stable, and confident everything is? That’s because there’s little conflict between the pitches, no complex vibrations.
Now let’s get dissonant:
These are more tense, less stable. You can hear a lot of conflict between the pitches, which makes these relatively dissonant. They “want” to resolve to a more consonant interval, which drives the drama in music. And the ratios are getting complex — 8:15, 8:9, and a wickedly cool √2:1, respectively.
That last one is especially interesting. It’s a tritone, an internal three whole steps across (hence the name). It divides the octave exactly in half, so you’d think it would be consonant. But when you can’t even express the ratio without resorting to irrational numbers, you know you’re not in Kansas anymore.
Sure enough, the extreme dissonance and instability of the tritone has been recognized for a thousand years at least. Monk and music theorist Guido d’Arezzo called it Diabolus in musica, “the Devil in music.” The tritone loved that and immediately had it tattooed on its lower note, at which point it was banned from church music for several centuries (true dat).
But before we make the leap from “tense and unstable” to “unpleasing,” let’s put them in context. Here’s a minor 2nd, first alone, then in context:
And here’s a tritone in two very different settings — one romantic, one funny:
See? Of course the tritone CAN be damned unpleasant when it needs to be. Turn it up to freak out your dog:
And here’s one you’ll recognize from childhood:
[arve url=”https://www.youtube.com/embed/Jtie6r27JeU” parameters=”start=26″ /]
The brass start with a tritone, then the Witch’s Guards come in singing a fifth — yo ee oh…yohhh, oh, or whatever. The combination is confident power (5th) + sinister threat (tritone).
But back to dissonance being amazing. Here are four short excerpts with nearly continuous dissonance. These are some of my favorite passages on the planet, so if you skip it, don’t tell me (under 3 min):
2. Bartok MSPC, mvt. II
3. Stravinsky, The Rite of Spring
4. Charles Mingus, Don’t Be Afraid, the Clown’s Afraid Too
And dissonance goes way beyond that. Epitaph for Moonlight by the Canadian composer Murray Shafer pushes pitch just about as far as it can go, and he does it with the human voice. Follow the pencil (4:38):
[arve url=”https://www.youtube.com/embed/l1SlyJ2kreI” /]
I know that’s not everyone’s cup, but boy is it mine.
Music without dissonance…well, just imagine a drama, or even a comedy, entirely devoid of conflict. That would be unpleasant. It might make for nice lunch conversation, but it doesn’t make for good theatre. In addition to being rich and beautiful on its own terms, we need dissonance to give consonance its raison d’être. Sliding the level of tension up and down the continuum of consonance and dissonance by combining pitches, intervals, and chords is one of the critical emotional tools of the composer.
And even if your tastes don’t run as dissonant as mine, believe me — you wouldn’t want to do without it.
Follow me on Facebook:
Isn’t It Iconic?
Image from Nirvana’s Nevermind album
A University of London researcher has found something we didn’t even know we were looking for: the most iconic song ever written. After announcing his choice, he was moved to an undisclosed location.
If the comment sections are any indication, a lot of the complaints are due to a misunderstanding about the researcher’s claim. He didn’t claim to have found the best song, or the most powerful, moving, or effective one. Dr. Mick Grierson was looking for the most iconic.
To qualify as iconic, he says, a song has to be well-known and distinctive. If it’s famous but very similar to a lot of others, it isn’t distinctive, so it can’t really be iconic. And a very distinctive song still isn’t iconic if few people have ever heard it. It might be to you, but not to the culture at large.
Even understanding that, I was mystified by the result — until I discovered something hiding in plain sight.
Grierson created a credible list of the 50 best-known songs using lists from magazines like Rolling Stone. To assess “distinctiveness,” he used computer software to analyze some elements of the music itself. Of the 50 songs:
- 80% are in a major key (mostly A, E, C and G)
- Average tempo is 125 beats per minute, a brisk walking tempo
- Average length is 4 minutes on the nose
- Average number of different chords is 6-8
He also looked at something he called “spectral flux,” which he said is “how the power of a note from one to the next varies.” I’m not sure what he means by that, but I’m guessing it has to do with variation in tone color and intensity.
Another variable called “tonic dissonance” apparently refers to the use of pitches outside of the key, i.e. non-harmonic tones.
So what he wanted was a song that was famous but departed from the norm in a number of these quantifiable ways. A minor key would count as departure, as would unusual tempo or length, or greater than average number of chord changes, or frequent changes of timbre, or a lot of pitches outside of the key.
So what song did he and his computer decide is the most iconic of all time? Nirvana’s 1991 hit Smells Like Teen Spirit.
I…wut.
I’m not one to howl when the particular headbanger anthem that got me through puberty doesn’t make somebody’s Top Ten list. I’m on the side of truth and justice for this one, no skin in the game. In fact, I really like Teen Spirit, especially the way the melody leans into unexpected pitches, and that contrast between quiet lethargy and full-throated entitlement. More emblematic of a generational moment than most songs making that claim. I can even see it in the top 50 iconics, why not. But by the study’s own stated variables — not just my preferences — I couldn’t understand how it qualified as Most Iconic.
Let’s compare Teen Spirit to two other songs that were lower on the list.
#1. Smells Like Teen Spirit – Nirvana (1991)
[arve url=”https://www.youtube.com/watch?v=UGqDQKLUXko” /]
Most of the top 50 are in a major key, and Teen Spirit is minor. One point for iconic.
The tempo is 116 beats a minute, close to the average of 125. The length is 4:35, just over the average of 4:00. Two points for typical.
Harmonic diversity is slim. Aside from the kind of silly 4-bar bridges at 1:23 and 2:38, the whole song appears to be the same four chords in the same order: F minor, Bb, Ab, and Db.
Hey wait a sec: they aren’t even chords. Chords have at least three pitches. These are something guitarists call “power chords,” a rock staple (i.e. “not iconic”) that removes the third from every chord. So instead of F-Ab-C, it’s just F-C, and so on. It’s a really powerful, raw sound, but it reduces the already poor pitch diversity even further.
If we take out the little 4-bar bridges — a total of 16 seconds — Teen Spirit doesn’t have even one pitch outside of the key, which is pretty low tonic dissonance. Include the bridges and it has just two such pitches.
Variation in timbre is there, but moderate. An effective toggle of atmospheres between the mumble and shout sections, but it’s still drums and guitars from start to finish.
I love the song, and it’s Top 50 iconic. But not #1.
#15. Stairway to Heaven – Led Zeppelin (1971)
Play a minute or two as you read:
[arve url=”https://www.youtube.com/watch?v=iXQUu5Dti4g” /]
Despite a minor key, a distinctive harmonic language, a rhapsodic structure, and an 8-minute duration (for which I and all other teenage slow-dancers of the 70s and 80s are grateful), this iconic rock song came in 15th.
Within seven seconds, Stairway has already exceeded Teen Spirit in harmonic variety. It starts with a progression of five different chords over that (yes) iconic chromatic bassline, including an augmented triad and a major-major 7th chord on VI.
Tempo structure is also unique. It starts at 76 beats a minute, way off the average. When the drums enter for the first time at 4:19…well, first of all you say, “No drums for four minutes and 19 seconds! How iconic!” Then the tempo picks up a click to 84. Around 6 minutes, it goes up to 96. It’s a nice effect, a slight acceleration over time that helps sustain the long form.
As for tone color, dynamics, and other “spectral” aspects, Stairway moves through multiple sections, from acoustic guitar and a consort of recorders (iconic!) to electric guitars and a shout chorus before ending in a quiet solo a cappella.
Finally: Did the researcher even try making out to Smells Like Teen Spirit? You’d end up on a pile of bloody teeth. Stairway for the win.
#5. Bohemian Rhapsody – Queen (1975)
Play a minute or two as you read:
[arve url=”https://www.youtube.com/embed/fJ9rUzIMcZQ” /]
For pure iconic differentness, it’s Bohemian Rhapsody in a walk. A six-part rhapsody form moves from a cappella ballad to Gilbert and Sullivan operetta to hard rock and back to ballad, changing key at every gate.
But we don’t even have to look that far to beat Teen Spirit. In the introduction alone, Rhapsody has nine different chords, including an added sixth chord (0:05), a secondary dominant 7th (0:09), chromatic neighbor chords (0:37), and a fully-diminished secondary leading tone 7th chord (0:47). AND it changes key after just 25 seconds.
Talk about awesome tonic dissonance –all that, and all 12 notes of the chromatic scale, and we’re less than one minute in.
The pretty obvious thing I missed about Teen Spirit
But wait a minute.
There’s another chord in Teen Spirit. It doesn’t show up in the chord charts, and it has always slipped right past my ear. It’s a chromatic passing chord, the very last thing you hear at the end of the first bar (4 sec):
[arve url=”https://www.youtube.com/watch?v=UGqDQKLUXko” parameters=”end=4″ /]
Tiny detail, right? It is to us humans. But here’s the thing: We’re in F minor, so both of those notes (E and A) are outside of the key. And it appears not once, but about fifty times, in alternating bars for most of the song! To you and me, it slides on by. But a computer analyzing for pitch variety will hear a song positively soaking in “tonic dissonance.”
Still, that’s only eight notes out of 12. We’re still missing Gb, G, B and D.
But wait! What about those two ugly notes in the bridge? (3 sec)
[arve url=”https://www.youtube.com/watch?v=UGqDQKLUXko” parameters=”start=91 end=93″ /]
Dude, no weh! It’s Gb and B. Add the excellent G Kurt is always leaning on
and Smells Like Teen Spirit has 11 of the 12 chromatic pitches, including a constant saturation of those two pitches outside of the key.
But here’s the thing: Except for the vocal G, they just aren’t significant. Unlike Bohemian Rhapsody, for example, the unusual pitches are mostly incidental — a passing tone on a weak beat. No matter how often it happens, it isn’t significant enough to raise a song to iconic status. Our brains can sort between significant pitches and incidental ones. But to a computer counting the frequency of frequencies, it’s all the same.
That’s why Smells Like Teen Spirit is the #1 most iconic song among Dell Inspirons.
The 50 most iconic songs, according to a computer
1. “Smells Like Teen Spirit,” Nirvana
2. “Imagine,” John Lennon
3. “One,” U2
4. “Billie Jean,” Michael Jackson
5. “Bohemian Rhapsody,” Queen
6. “Hey Jude,” The Beatles
7. “Like A Rolling Stone,” Bob Dylan
8. “I Can’t Get No Satisfaction,” Rolling Stones
9. “God Save The Queen,” Sex Pistols
10. “Sweet Child O’ Mine,” Guns N’ Roses
11. “London Calling,” The Clash
12. “Waterloo Sunset,” The Kinks
13. “Hotel California,” The Eagles
14. “Your Song,” Elton John
15. “Stairway To Heaven,” Led Zeppelin
16. “The Twist,” Chubby Checker
17. “Live Forever,” Oasis
18. “I Will Always Love You,” Whitney Houston
19. “Life On Mars?” David Bowie
20. “Heartbreak Hotel,” Elvis Presley
21. “Over The Rainbow,” Judy Garland
22. “What’s Goin’ On,” Marvin Gaye
23. “Born To Run,” Bruce Springsteen
24. “Be My Baby,” The Ronettes
25. “Creep,” Radiohead
26. “Bridge Over Troubled Water,” Simon & Garfunkel
27. “Respect,” Aretha Franklin
28. “Family Affair,” Sly And The Family Stone
29. “Dancing Queen,” ABBA
30. “Good Vibrations,” The Beach Boys
31. “Purple Haze,” Jimi Hendrix
32. “Yesterday,” The Beatles
33. “Jonny B Goode,” Chuck Berry
34. “No Woman No Cry,” Bob Marley
35. “Hallelujah,” Jeff Buckley
36. “Every Breath You Take,” The Police
37. “A Day In The Life,” The Beatles
38. “Stand By Me,” Ben E King
39. “Papa’s Got A Brand New Bag,” James Brown
40. “Gimme Shelter,” The Rolling Stones
41. “What’d I Say,” Ray Charles
42. “Sultans Of Swing,” Dire Straits
43. “God Only Knows,” The Beach Boys
44. “You’ve Lost That Lovin’ Feeling,” The Righteous Brothers
45. “My Generation,” The Who
46. “Dancing In The Street,” Martha Reeves and the Vandellas
47. “When Doves Cry,” Prince
48. “A Change Is Gonna Come,” Sam Cooke
49. “River Deep Mountain High,” Ike and Tina Turner
50. “Best Of My Love,” The Emotions
Click LIKE below to follow Dale McGowan on Facebook!
The Greatest Mashup Ever: Why it Works
I love transformation, taking an existing thing and making something new out of it. It doesn’t always work. Sometimes it adds nothing to the original, and sometimes it’s a freakish horror that should never have seen the light of day.
But when it works, it can be gorgeous. Earth Wind and Fire’s “Got to Get You Into My Life.” Beethoven’s Diabelli Variations. Soderbergh’s Ocean’s Eleven.
Mashups take it to another level as two or more existing songs are slammed together. And again, the results vary from terrible to pointless to good to THE GREATEST THING I HAVE EVER EXPERIENCED EVER OMG.
Let’s look at that one.
The Greatest Mashup Ever Created, End of Conversation™ brings two hideously different songs together: Taylor Swift’s caffeinated pop-tart “Shake It Off,” and the gothic shadow-world of “The Perfect Drug” by Trent Reznor of Nine Inch Nails.
First the originals. For maximum appreciation of the mash, I suggest watching both of them first, but I am not the boss of you.
[arve url=”https://www.youtube.com/embed/nfWlot6h_JM” /]
[arve url=”https://www.youtube.com/embed/sSLqeZzTU8I” /]
And now…Taylor Swift vs. Nine Inch Nails, by mashup artist Isosine.
[arve url=”https://www.youtube.com/embed/DhvXST1Rc3g” /]
Why It Works
The Lucky Coincidence
The two originals are not only close in tempo and key, but “Drug” is both a little slower than “Shake” (150 vs. 160 beats per minute) and a little lower in key (F major vs. G major). So by slightly speeding up “Drug” and slightly slowing down “Shake,” he brings both tempo and pitch into sync. The mashup is right smack in the middle of the two, 155 bpm and F# major. If they were further apart in pitch or tempo, at least one of the originals would have to be sped up or slowed down too far to work as well.
The New Story
The most common comment on the mashup is, “This shouldn’t work, but somehow it does.” There is no somehow. The opposition is a big part of why it works. There’s nothing new about contrasting light and dark, happy and grim. But this mashup combines the moods and themes of the two songs to create a third scenario. “Perfect Drug” is about an unnamed second-person obsession — You are the perfect drug. In the mashup, Swift becomes the “you,” the subject. The resulting narrative is instantly recognizable: She is the pretty, popular girl, the center of a cloud of beautiful people who move and dress and exist effortlessly at the top of the social pyramid. He’s the brooding obsessive loner, his attention fixed solely on her. She sings and dances, oblivious to his fixation, and his frustration grows.
At one point (1:15) she maddeningly seems to dance to his music as he sings The arrow goes straight to my heart/Without you everything just falls apart. At another, Swift’s trademark look of shocked surprise (1:37) is no longer about the row of jiggling butts behind her, but about his repeated line, And I want you. And yes, in this narrative, the icicle-dagger at 1:44 is especially creepy.
(As an antidote, there’s a nice comic touch when she sings “the fella over there with the hella good hair” (2:40) and it flashes to a greasy, glum Reznor.)
The Music
“Perfect Drug” is conveniently non-tonal for long stretches — it doesn’t get a tonal center at all for the first 50 seconds as he chants lyrics tunelessly against that cool, unsettling microtonal string thing. That allows Isosine to lay it over the Swift without worrying about pitch for about the first minute.
But they connect in other ways. Compare the rhythm in Reznor’s lyric to the rhythm in Swift’s bari sax (7 sec):
[arve url=”https://www.youtube.com/embed/DhvXST1Rc3g” parameters=”start=06 end=13″ /]
For the first 30 seconds of the mash, those two insanely well-matched rhythmic motives knit the two songs together musically, sounding as if they were made to be together.
With a slight nudge of the fader, Isosine creates another jigsaw fit in the next 12 seconds: Swift’s melody lays in the first and third bars of each phrase, while Reznor’s lyrics are in the second and fourth bars, reiterating his obsession four times with increasing intensity (13 sec):
[arve url=”https://www.youtube.com/embed/DhvXST1Rc3g” parameters=”start=30 end=44″ /]
And when “Perfect Drug” finally does go tonal in the refrain You are the perfect drug, the perfect drug, it works seamlessly with the bass and harmony of the Swift.
There’s more — there’s always more — but I’ll turn it over to you.
Trivia Bonus: The music videos for “Perfect Drug” and “Shake It Off” were (oddly) both directed by the same guy — filmmaker Mark Romanek.
Thanks to Paul Fidalgo, who first brought this mashup to my attention on his excellent blog iMortal.
Radiohead: What IS that note?
Years ago, when I taught music theory, I’d ask students to bring in recordings of music they loved. We’d play a minute of something, then talk for a few more minutes about what was going on there. Applied theory, always my favorite part of the class.
One day, a student in the class gave me one of the best musical gifts I’ve ever received. She introduced me to Radiohead.
The song was Paranoid Android, and I knew within the first minute that we wouldn’t do anything else that day. But this post isn’t about Paranoid Android. It’s about another Radiohead song, one that uses the ideas in the post about scales, the fact that octaves can be broken up an infinite number of ways, including exotic sequences of steps producing unique emotional palettes that are different from the major and minor we’re used to hearing. There are even microtonal pitches that would fall in the cracks of a piano keyboard if they were foolish enough to wander onto one. It’s the atmospheric masterpiece How To Disappear Completely.
Listen first (5:56):
[arve url=”https://www.youtube.com/embed/nZq_jeYsbTs” /]
Damn.
There are a hundred things to talk about in there, like that cool, quiet walking bass that starts around 0:21, cutting across the guitar in a laid-back polyrhythm. But let’s look at what he’s doing with pitch, especially the scale and the use of microtones.
The song is in F# not-quite-minor. Six of the seven steps in the scale got the memo for F# minor — F#, A, B, C#, D, E — but the second note, which should be G#, is G-natural instead, just a half step above the key note. That’s one of the things that made the Byzantine scale sound exotic. But this time the scale is F# [tippy title=”Phrygian”]More about Phrygian later, when we get to modes.[/tippy], which has this nice dark quality. When he sings In a little while, I’ll be gone, listen to the note on I’ll. That’s the lowered second, that G-natural (excerpt 19 sec):
[arve url=”https://www.youtube.com/embed/nZq_jeYsbTs” parameters=”start=133 end=152″ /]
He really leans into it later on as the whole chord, not just one note, is on G (excerpt 36 sec):
[arve url=”https://www.youtube.com/embed/nZq_jeYsbTs” parameters=”start=210 end=246″ /]
You four-pepper theory types may notice that the bass is still on the same pitches under the G chord that it played under the VI-i progression in f#m earlier. That’s a basso ostinato (literally “obstinate bass”) — the bass sees no reason to change just because the chord above it has. The result is a gorgeous harmonic mix.The microtonality happens mostly in the sliding mush of strings later on. I especially love the moment when he has you whirling in a microtonal cloud of strings, then suddenly POP — the cloud disperses and you’re back in the clear tonally (excerpt 24 sec):
[arve url=”https://www.youtube.com/embed/nZq_jeYsbTs” parameters=”start=302 end=326″ /]
Just a stunning effect. But my favorite thing about this amazing song is one note — that high siren in the distance at the start. It’s a note to haunt your dreams. What the hell is up with that note? (excerpt 23 sec)
[arve url=”https://www.youtube.com/embed/nZq_jeYsbTs” parameters=”end=23″ /]
It took me a long time to realize why that pitch sounded so otherworldly: It’s not even a pitch in the scale. It’s a microtone, a pitch in the crack between A and A#.
But even before I figured that out, it worked. And that distant, haunting siren is still a big part of what makes this astonishing piece work for me.
Follow on Facebook…
Thom Yorke portrait by John LeMasney via Flickr | CC A-SA 2.0 Generic
Jonny Greenwood thumbnail by angela n. via Flickr | CC BY 2.0
Scales! Wait. Come back.
I hated scales in middle school. Oh I was good at scales, even got a certificate for playing all four forms of every scale by memory on my wee clarinet. I was a good boy.
And still I hated them.
It just seemed like such a pointless, hoop-jumping thing to me. Memorize these note patterns, then play each one starting from every possible note, and you win. But aside from the value of rote memorization and the fingering practice…what was the point?
There were other unanswered questions in my head — like Why are there three different kinds of minor scales? Why is the melodic minor different going up and going down? Why does the harmonic minor make me sound like a snake charmer? Why does minor sound sad and major sound happy? Are these the only four ways to get from C to C?
It’s like the Steven Wright joke
Why is the alphabet in that order? Is it because of that song?
Scales are actually cool and interesting once you know what they’re for. Stick with me to the end of the post, then tell me if I’m wrong. (Spoiler: I’m not.)
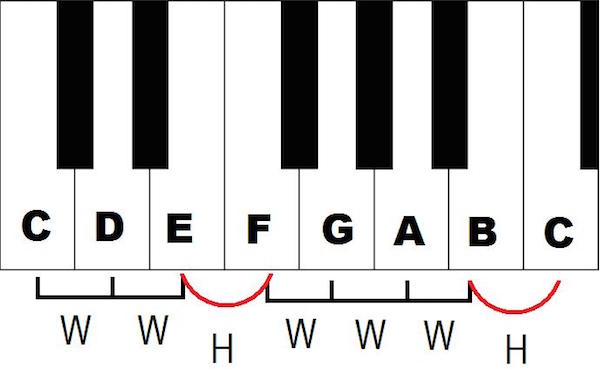
Last time I split the octave into 12 equal parts to make the chromatic scale. The name hints at the purpose. By containing all 12 of the pitches we use in Western music, the chromatic scale is like a paint store with 12 available colors.
You don’t want every available color for a painting project. You choose a palette — a subset of colors, a theme. If you want this result:
…don’t use every color in the store. Use this palette:
Same for music. The chromatic scale has every available pitch in the Western tonal system. The distance from one to the next is a half step. Here are the 12 half steps of the chromatic scale (plus the next C):
When I write a piece, I don’t need every note. If I want a certain mood, I’ll choose a subset of pitches from the 12 available, and a different subset gets me a different mood.
Example: If I choose every other pitch, instead of 12 notes a half step apart, I’ll have 6 notes a whole step apart. That’s called a whole tone scale:
There’s something strange about that scale, right? It starts going off the rails at the 4th note and never gets normal again. Here’s why: All of the pitches are the same distance apart. No half steps. Because of that, your ear can’t easily track where you are. Aside from whatever note we happen to start on, none of the pitches stands out as “home,” so the whole tone scale creates music with an ethereal, directionless quality. If you were a child of the 70s, you know it well. Whenever there was a campy flashback in The Brady Bunch, or Scooby Doo was being hypnotized, there’s a good chance a harp or bells were playing music drawn from a whole tone scale:
One particular Debussy piano piece called Voiles (Sails) is the go-to for illustrating a whole tone scale. Feel that unanchored, homeless quality (0:47):
[arve url=”https://www.youtube.com/watch?v=95_OvaRHwDg” parameters=”start=9 end=56″ /]
The fact that pretty much every theory teacher uses sitcom flashbacks and one Debussy piece as whole tone examples shows you just how rare it is. Beyond drifty sails and coming unstuck in time, a scale with all the pitches equally spaced just isn’t all that useful. If someone gave you driving directions like this — Go one block and left, one block and right, one block and right, one block and left, one block and right, and on and on across town, you’d have a helluva time finding your way home again. Every step is the same. It’s confusing.
If instead the directions were Go one block and left, three blocks and right, one block and left, then five blocks and you’re there — now the steps are different enough to landmark in your head. You need a scale that works the same way — a mix of steps of different sizes so your ear knows where you are relative to home.
Major and minor scales do just that, creating a pattern of pitches that are different distances apart. They do it by choosing only 7 of the 12 notes, leaving gaps where the other pitches were. The scale shows the ladder of steps between the notes if you arrange them in order. Here’s a C major scale:
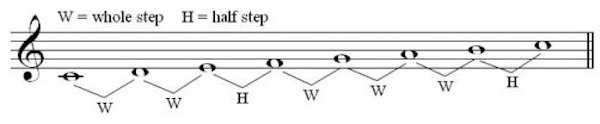
You start on C but leave out C# and go to D — a whole step. It’s like going from red to orange and skipping reddish-orange. The major scale then goes another whole step (to E), then a half step (F), then three more whole steps (G-A-B), and finally a half step to the next C. If you start on C, the white keys on a piano fall naturally into the major scale without any adjustments. The black keys are the gaps, the five chromatic pitches that were left out of the major scale:
If you start on a note other than C, you’ll have to raise or lower notes along the way, using flats and sharps on the page and black keys on the piano to get the same pattern of whole steps and half steps.
Scales aren’t meant to be played in that order any more than the letters in a word are supposed to be spelled out in alphabetical order, or a set of colors in your paint theme is supposed to be painted left to right on the wall by wavelength. Hey, rainbows are great, but you don’t want a rainbow every time you paint. So when you paint your house, this is the scale:
…and this is the music:
The scale is a set of instructions to pick out the colors (pitches) that establish a certain palette (key) for the music you want to write.
But music goes beyond the visual analogy to something that makes its emotional power possible. This pattern also creates a kind of aural map. The sequence of half and whole steps sticks a pin in one of the notes, calling it home, then creates a series of landmarks to tell you where you are relative to that home at all times. By listening to music all your life, your ear has learned how to follow that map — to go away from home, have adventures, and return (or not). The next three JET posts will get into that.
The minor scale is a different pattern of whole steps and half steps spanning the octave. The result is a different emotional palette:
The minor scale results when you lower the third, sixth, and seventh pitches of the major. That’s worth remembering. No need to memorizing key signatures or build scales yourself, but we’ll certainly talk about the various shenanigans the third, sixth, and seventh notes of the scale get up to.
Three great scales from elsewhere
Step outside of Western music and you can really start to see how different scales color the music. I hinted at that last time with the Carnatic microtonal scales. (Don’t be skipping stuff, or all is lost.) Here are three more.
Arabic music has at least 90 different scales, or maqam, each of which provides a different mood. Here’s one, maqam nawa athar:
Which sounds like this:
Hear that? It’s just crammed with intervals that sound exotic to Western ears. If a major scale is a map across your hometown, this one is a map to the market in Marrakech.
Several of the pitches of the Indonesian pelog scale fall in the gaps between our notes, which further shows that all scale divisions are arbitrary and cultural. You can’t even notate pelog properly with Western notation. If you try, you end up with these apologetic little plus and minus signs to indicate “a little higher” or “a little lower” than the notation:
And why not? Remember the sixth overtone, the B-extra-flat? To Western listeners, these pitches sound out of tune because they don’t match our particular divisions, but they have no less claim. Here’s pelog:
And here’s a phenomenal Balinese gamelan playing music using a variant of pelog. If you haven’t heard Balinese gamelan before, strap in, this is awesome:
[arve url=”https://www.youtube.com/watch?v=ldPMifPbngc” /]
Want to evoke a Middle Eastern vibe? Use the Byzantine scale:
It starts with a half step, which is instantly exotic (neither major nor minor does that), and twice again you get that wide step and a half (the ties above). The composer Saint-Saëns knew he could throw you into the ancient Levant for his opera Samson and Delilah by using the Byzantine scale:
[arve url=”https://www.youtube.com/watch?v=TEhor3HeulE” parameters=”start=9 end=34″ /]
Other minors and the modes down the road. Now go outside and play.
Pitch: Slicing up infinity
The electromagnetic spectrum covers a huge span of wavelengths, from a trillionth of a meter to (hypothetically) the size of the universe. Most of this energy — gamma rays, X-rays, microwaves, ultraviolet, and so on — is invisible. But a tiny sliver is visible light:
Different wavelengths within that tiny window present as different colors. Newton first described the rainbow as having five colors — purple, blue, green, yellow, and red. He later added orange and indigo for a silly reason I’ll describe in a minute. Neither answer was wrong, and neither was right.
When I was six, my box of crayons had eight colors. By the time I was ten, there were 64. The crayonic scientists hadn’t discovered 56 more colors — they just split the spectrum into finer divisions, adding colors like blue-green and green-blue. (Some speak of a 120-color Crayola box, but the few photos that exist are suspiciously blurry.)
My first color computer monitor displayed 256 colors. The one I’m on now has the weirdly non-specific “millions of colors.” The possible colors in that spectrum are literally infinite: Just as you can endlessly divide a number line into smaller and smaller fractions, you can tweak wavelengths forever. So instead of being handed a specific natural palette, we divide the spectrum up arbitrarily to meet our needs: five colors in the rainbow, or seven; eight crayons or 64; 256 colors on the monitor, or millions; and 1500 choices in the Sherwin-Williams store. Until you mix a speck of mauve into the gallon of Carnival Orange and get 1,501.
Sound works the same as color. The range of frequencies we can hear is a sliver of the possible range of vibrations. Here’s the full range that the average human can hear, from 20Hz to 20,000Hz:
[arve url=”https://www.youtube.com/embed/qNf9nzvnd1k” /]
Like color, pitch is infinitely divisible, so we make choices about how finely to slice up that spectrum of sound. But one division is so basic to the physics of sound that it serves as the starting point for pretty much every music system on Earth: the octave. Give us an octave, Dorothy:
[arve url=”https://www.youtube.com/embed/PSZxmZmBfnU” parameters=”start=0 end=3″ /]
Doubling any vibration sends you up one octave, and the octave is the relationship between any note and its first overtone. It’s the strongest pitch relationship in music, and you can hear the family resemblance. In Western music, we designate that close relationship with a letter name. Notes vibrating at 110, 220, 440, and 880Hz are all “A,” for example.
So octaves are basic. But using octaves as the only musical steps would make for pretty poor music, like painting with 50 shades of grey. We want additional pitches to use, smaller divisions to give us more of the available colors. How small is the question.
There’s a slightly hilarious psych term for the amount something has to change before the average person will notice. You’d think it would be the “minimum discernment threshold” (MDT) or something similarly sciencey, but no: It’s the JND — the Just-Noticeable Difference. When my wife gets a haircut, it’s often a JND experiment for me.
The concept reaches even beyond haircuts to the perception of things like color and pitch.
That audible range from 20Hz to 20KHz is about 10 octaves. (For comparison, the piano keyboard is just over 7 octaves.) We could split the full range of human hearing into a maximum of about 1,400 just-noticeably-different pitches — 140 pitches per octave. But just as octaves are too big to be our only interval, these are way too small to make musical sense. Going from one to the next sounds more like drifting very slightly out of tune than anything musically useful.
So over time, instead of using 140 pitches in the octave that are barely noticeable in their differences, music cultures have divided up the octave into fewer, more useful and noticeable pitch differences.
South Indian Carnatic music uses the term śruti (or shruti) for the smallest meaningful interval of pitch. Some Carnatic theorists have put that number as high as 66 pitches in the octave, but Carnatic practice actually uses 22 — still a lot of small steps to Western ears. The result is some amazingly nuanced, slippery melodic contours.
Listen to the tiny pitch differences in this performance. The string drone establishes a central pitch, like the Western tonic. The singer’s voice dances in the amazingly tight Carnatic spaces around that center. Just before the midpoint of the clip, she locks in with the drone, then dances away again, returning home once more at the end (58sec):
[arve url=”https://www.youtube.com/watch?v=s5a3pthL_tU” parameters=”start=9 end=75″ /]
Western music settled on 12 pitches, equally spaced about twice as far apart as the Carnatic śruti:
That’s the arbitrary paint store that provides pitches for nearly all Western music — folk tunes, opera, rock, pop, everything. It’s called a chromatic scale, which is perfect — chroma is Greek for color, and scala is Italian for ladder or steps. It isn’t music any more than a paint store is a painting. It’s the resource we draw on to create music.
As the Carnatic example shows, the octave can be divided up any number of other ways. There are big gaps between those notes in the chromatic scale, and there could be notes in those spaces, or in some of those spaces but not others. The composer Harry Partch built his own instruments to bust out of the constraints of the Western pitch ladder. Try this on for a minute:
Several more recent inventions like the fluid piano and tonal plexus have also poked around in those pitch gaps. (If you love this kind of boundary-pushing, find 17 minutes for this stunning soundscape by Wendy Carlos.)
Instead of finding more pitches in the cracks of the chromatic scale, we usually go the other way, taking pitches away from the 12 and playing around with what remains. You can get a scale with steps of various sizes that way. Even the 22-pitch Carnatic system doesn’t treat all 22 as equal players in a given piece. There’s a subset that provides the melodic backbone, and the rest serve as ornaments and variants.
Newton’s wheel, with colors analogous to pitches in the major scale. Different-sized pie wedges equal different intervals in the scale.
The Western major scale works the same way, using seven of the 12 pitches as the backbone of melody and harmony — that’s your do re mi fa sol la ti. The other five pitches are “non-diatonic,” meaning outside of the key, and are used as ornaments and variants — delightful, delicious ornaments and variants.
The seven-note major scale, by the way, is why Newton added orange and indigo to make seven colors in the rainbow. He was enamored of the Pythagorean idea of a “harmony of the universe” (musica universalis) and thought the rainbow ought to reflect the pitches of the musical scale, as well as the known objects in the solar system at the time and even the days of the week.
Never mind that the scale and the week are also arbitrary and the astronomical count turned out incorrect — it’s a thing we do, grabbing on to patterns and relationships to make sense of things. But the divisions themselves are neither right nor wrong — just useful.
More on the pitch/color connection:
The man who heard his paintbox hiss (the synaesthesia of Kandinsky)
Music for Measure: on the 300th Anniversary of Newton’s ‘Opticks’
Follow Dale on Facebook:
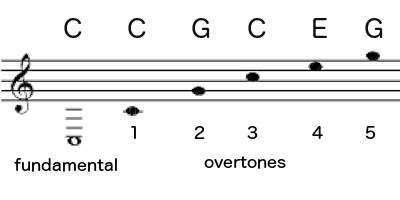
Overtones: Every note is a chord
Listen to this:
That’s a low C, a single note played on a piano. At least that’s how I’d have described it when I was 13. Within a year I was hearing that very differently, thanks to two great musicians.
One was my older brother Ron, who started playing piano when he was seven and I was three. I grew up in his shadow, musically and literally, laying by his feet while he played Chopin and Ravel, Scott Joplin and West Side Story (which he can still shred). He led me to Elton John and Genesis (until Genesis betrayed all that was good) and Jesus Christ Superstar. When I said The Rite of Spring was just noise, he ordered me to put the headphones on and listen again. And then I couldn’t stop.
When I was 14, Ron introduced me to my second huge musical influence by bringing home a set of LPs from the library. It wasn’t music, but a lecture series about music: Leonard Bernstein’s 1973 Norton Lectures at Harvard.
What Carl Sagan did for me with science, Bernstein did with music. I’d never heard anybody talk about music like Bernstein did in those lectures. He went below the surface in a way that was completely new to me. It was the start of my interest in music theory, which turned into a major, my first career, and a lifelong fascination.
The topic Bernstein covers first is the most stunning of all — that a single pitch contains an infinite number of pitches.
This isn’t an abstraction. These other pitches are tangible, and that matters. It’s one of the hidden keys to the ability of music to communicate emotions. But for reasons I’ve never understood, most of the current top-selling music theory textbooks never talk about it at all.
Actually, I do know why they leave it out: it isn’t necessary. It’s merely wonderful.
Don’t Skip the Miracle
Sound results from vibrations. The more regular the vibrating body is in structure — tuning fork, metal string, column of air — the less like noise the sound will be, and the more distinctively “pitched” and musical it sounds. The faster the vibration, the higher the pitch. As you go from left to right on the piano keyboard, you go from low to high, the strings get shorter and therefore vibrate faster, and the pitch gets higher.
The low C at the top of the post resulted when a felt hammer hit a string of a certain length in my piano. The string vibrated about 100 times a second (100 Hertz, or 100 Hz) along its entire length to produce that pitch.
If you double the speed of vibration to 200 Hz, the pitch goes up one octave to the next higher C. A string half as long will do this.
To go up another octave to the next C, just double the vibration again to 400 times a second. A string a fourth as long as the original one will vibrate four times faster, and you’ve got the next C.
And on it goes, with Cs at 800, 1600, 3200. You can hear the family resemblance between notes that are an octave apart. They’re like higher and lower versions of each other because of this simple ratio. If men and boys sing the same melody at the same time, they will tend to be an octave apart. But it doesn’t sound like they’re singing two different parts — just the same melody doubled at the octave. That’s how close the family resemblance is.
Play the low C again.
That string is vibrating at about 100 Hz along its entire length to produce the pitch C. Here’s a schematic of the string in vibration along its entire length:
Now here’s where it gets strange: at the same time it’s vibrating along its full length, the two halves of that string are vibrating independently. And because they’re half as long, they’re going twice as fast (200 Hz). Don’t ask me how this works — magic, I assume. We know that doubling the vibration sends the pitch up an octave. So in addition to the low C, you are also hearing the C an octave higher at the same time.
String vibrating in halves
Again, I’m not saying you are “hearing it,” in quotes, like it’s some hypothetical thing. When you play a low C, you are also actually hearing the C an octave higher. It’s a small but audible fraction of the sound. The note you’re playing is called the fundamental. The higher C is the first overtone. But because the two Cs have such a strong family resemblance, it’s hard to hear it. They are too similar.
Fortunately the string is also vibrating in thirds, at 300 Hz. That produces a G, the second overtone, which is usually pretty clear. Here’s the pitch for G, so you can get it in your ear:
String vibrating in thirds
The string is also vibrating in fourths (400 Hz), which is four times as fast as the low C and twice as fast as the second C, so that produces yet another C, an octave higher still:
And also in fifths (500 Hz), which produces an E. This one will be fainter, but because it’s not another C, you can usually hear it. Here’s the pitch to listen for:
And also in sixths (600 Hz), which is twice as fast as the G, so that’s another, higher G:
The divisions of the string continue infinitely in smaller and smaller intervals, all vibrating simultaneously and producing an infinite number of pitches. But after about the fifth overtone, the vibrations are such a tiny sliver of the sound that you usually can’t hear them.
No worries, we’ve already achieved the magic. When you play a C, you actually hear all of these pitches:
I don’t mean to startle you, but that’s a C major chord. When you play a C, you don’t just hear a C, you hear the pitches of a C major chord — C, E, and G. It’s not only C that does this, of course — play any pitch, and you are actually hearing not just that pitch, but a major chord based on that pitch. It’s more subtle than that recording, but you can hear it, and we will shortly.
We could do the same with any pitch: A, F#, Bb, anything. Because of the physics of vibration, each of them produces its own major chord.
Why do overtones matter? Because the emotional fuel of music is the interaction between pitches sounding simultaneously — harmony. And when you play any two pitches, it isn’t just those two pitches interacting – there’s a whole cloud of other notes above them interacting as well. (More on this when we get to consonance and dissonance.)
Now it’s time to hear the overtones, not as bells outlined on my synthesizer, but coming out of an actual single pitch. Turn the volume up a little. A lot of things affect how strongly overtones pop out when you play a note, including humidity and whether the piano is in tune. My piano is not, but the day was humid, so we’ll see what happens. I’ll play that low C one more time, and you listen for the second and fourth overtones (G and E) blooming out of the sound:
Oh man, this was a good day for overtones. The G blooms out almost immediately. The E and the next G become audible around 4 seconds. And right around 5 seconds…
Oh my. (Whispery teacher voice.) Boys and girls, we have a very special guest today. Around the 5-second mark, you begin to hear an overtone that is usually not audible — the sixth overtone, which results from the string vibrating in sevenths. This one’s an oddball to Western ears because it doesn’t correspond to an actual pitch we use. It lands in the crack between A and B-flat on the piano. But there it is, ringing out all the way to the end like it has no shame:
(Now go back and play the C again. Did you hear the B-extra-flat, especially after the others have died out a bit? It can help if you whistle or hum the pitch you’re looking for.)
Don’t be sad and scared if you can’t hear the overtones right away. You will eventually, and once you do, you’ll get quicker at it. It’s like those Magic Eye stereograms from the 90s where you [tippy title=”make your eyes go wonky”]Start with the image an inch from your nose. Gradually pull it back without adjusting your eyes.[/tippy] and boom, you see a space shuttle or the Mona Lisa or whatever:
See it?
Your assignment: Get to an actual piano. Thump that low C and hold it down. As the fundamental pitch decays, the overtones will bloom out of the sound, especially the G and E. If you’re lucky, you’ll even spot the exotic B-extra-flat.
Extra credit: Nine minutes of Leonard Bernstein demonstrating the same thing in a slightly different way. These are from the actual Harvard lectures I heard on LPs at 14.
[arve url=”https://www.youtube.com/watch?v=8n3qMB6AD_0″ /]
[arve url=”https://www.youtube.com/watch?v=iDTj6tBnHlA” /]
Can you hear the overtones? Tell me in the comments.
(Next post: Pitch.)
Click LIKE below to follow Dale McGowan on Facebook!
The Music That Broke My Heart
- September 01, 2015
- By Dale McGowan
- In Intro
1
During the weeks of shock and grief after the attacks of September 11, 2001, one piece of music was added to the programs of over 50 American symphony orchestras: Samuel Barber’s Adagio for Strings.
Vedran Smailović, “Cellist of Sarajevo,” in the ruins of the National Library, 1992
This piece was already special to me. When I first heard it at 18, I cried uncontrollably. It wasn’t just generally “sad” for me — it seemed to bring out the exact sequence of emotions I’d felt after the death of my dad five years earlier. I felt my grief unfolding in a painfully familiar way.
What the hell? There were no evocative lyrics, no title like “Death of a Dad” to prime my emotional pump — just pitches arranged over time, played by a string orchestra.
Five years later, after studying music theory in college, I sat down with the Adagio to figure out how Barber had communicated grief so effectively.
After a few minutes with the score, I saw what he’d done. It was brilliant, something anyone could understand if they just had a little [tippy title=”music theory”]The study of the grammar, syntax, and semantics of music.[/tippy]. Just a little music theory is all you need to unlock this emotional language and know how music works. Of course the great thing is that it works even if you don’t know how it does.
But oh, the knowing.
When the Adagio was added to the programs of all those orchestras after 9/11, NPR invited a “cultural commentator” to explain what it was about that particular piece that captured grief so well for so many people. Given his answer, he should have said, “Beats me.” Instead, he said roughly this:
When President Roosevelt died in 1945, the funeral planners went looking for appropriate music for his service. They knew they wanted something slow and beautiful. Barber’s Adagio, which was written just a few years earlier, was slow and beautiful, and it was selected for the funeral. Eighteen years later, the piece was played again for the funeral of JFK, in part because it had been in FDR’s funeral. From that point forward, Barber’s Adagio became associated with sadness in the national mind.
I was slack-jawed. He flipped the cause and effect. It’s like saying the 23rd Psalm is comforting because it’s been used to comfort people for so long. It’s like saying Tabasco sauce is considered hot because it’s in Cajun food.
Neither psalm nor sauce nor Adagio became what it is by association alone. In each case, most of what hits us is in the thing itself.
Tragedy, desperation, false hope, and exhausted resignation are all woven into the music of the Adagio, which then reaches me because my brain recognizes the emotional language in which it’s written. I knew how Barber had done it. But NPR never called, so I explained it to my dog.
He was impressed.
Eight years later, conductor and composer Rob Kapilow was talking about the Adagio on NPR for the Barber centennial. He said the kind of catharsis the piece goes through is similar to the catharsis at a funeral:
It starts from incredible sadness, builds to an incredible climax of intensity, and then finally reaches a kind of serene acceptance, which is completely appropriate for those occasions.
That’s good stuff. He’s talking funerals again, but he’s not saying funerals caused the music to sound sad. He’s saying the music parallels the emotional process in grief, which it does. Now he’ll talk about what makes the sadness, and what underpins that climax — the [tippy title=”harmony”]The relationship of pitches sounding at the same time.[/tippy].
It starts off with just a single note. And it’s so pure, it’s as if that note somehow was there forever.
That’s neat. Now talk about the harmony.
So Barber lets you sit there, with that one note on the violin, for an incredibly long time, and then the note gets drenched with the emotion of a rich chord in the strings. Finally it has to move, and it starts this lovely first phrase, which seems to take forever.
Yes, there is much foreverness. Now talk about the harmony. He knows what that “rich chord” is, of course — Kapilow’s an Eastman-trained composer. He just doesn’t think he can explain it to the layperson within the limits of a radio program. But this is NPR, dammit. That’s what they do.
He doesn’t have to say it’s a subdominant minor-minor seventh chord. But he can say this: Because of the grammar of music you’ve grown up hearing, the first two chords create an arrow of harmony that points your ears to a very specific place you don’t want to go. Then the next two chords suddenly lift you out of danger like a helicopter taking you off the roof.
Then you play those 30 seconds, and you can feel it happening.
In the next 30 seconds, after a moment of relief, you feel yourself sinking back to where we started — the same two chords, that harmonic arrow to despair. The escape didn’t work. Silence — then you try again.
But he doesn’t talk about harmony (notes played simultaneously). He talks about melody (notes played in sequence):
You have a sequence of three notes up, three notes up again, then you do it up a step. Then you do it again. And then … just, stop. The simplest pattern. A whole second wing of copying the pattern starts in the violas. Gradually, the slow repetitions acquire more expression and emotion. The piece gets higher and fuller.
It’s all true. The three-note, repeating-and-rising thing is very nice. But talking about the three-note melodic pattern as if it’s The Thing is like explaining the effectiveness of the “I Have a Dream” speech by describing Martin Luther King’s hand gestures. That’s part of what made the speech work, I suppose, but you can’t talk about why that speech became the iconic King speech without looking at the content, and the meaning that content conveyed.
In language, the primary (though not exclusive) vehicle of meaning is words and sentences. In [tippy title=”music”](i.e. Western tonal music).[/tippy], the primary vehicle of meaning is chords and chord progressions — the harmony.
He continues:
The simplicity of the logic is to make you feel the universality of the journey: from the simple note to the high emotional wailing to release and to final acceptance, but never in the place you thought it was going to lead you to.
Oo! That last bit was good. And what was that unexpected place? Not an unexpected three-note pattern. Not a sudden naked bagpipe solo. It takes you somewhere that’s harmonically unexpected. And if you (like me) were raised hearing the syntax and semantics of Western music, then Barber is speaking your language, and you feel it.
Yes, you need to know music theory to understand the harmonic language of music. But here’s the thing: you don’t need a lot of theory. You need just enough theory to unlock what’s going on. Maybe that’s still too much for a five-minute radio piece to get into, but a blog stretches to the horizon. We can even go beyond the theory to the fascinating intersection of physics, biology, culture, and personal experience that makes the emotional language of music comprehensible for one person or group but not another. So here we are, with you deciding whether to keep reading.
Keep reading.
If you’re willing to put in the effort to learn just enough theory, I’d love to share it. The basics will take about 12 posts, and I’ll scatter a lot of music in there as well. Then once we’ve covered the basics, we can talk about music in a whole new way, which is what the blog will do forever. For reference, the original teaching posts will always be in the right sidebar under the heading Just Enough Theory. I’ve also added a hover feature so you can get the definitions of a few key terms in any post. [tippy title=”Hover over any text with a blue dotted underline, like this…”]…and a quick definition or comment will pop up.[/tippy]
At some point, I’ll circle back and talk about the Adagio in great detail, but not for a while. First we’ll apply music theory to a lot of other music, especially music you suggest. To allow time for conversation in the comments, posts will be weekly for a while, then I’ll pick up the pace.
To play us out, here’s Leonard Slatkin and the St. Louis Symphony with the piece that made me want to know how music does that.
[arve url=”https://www.youtube.com/watch?v=wBK30bJagEA” /]
Click LIKE below to follow Dale McGowan on Facebook!
Photo of Vedran Smailović by Mikhail Evstafiev. Licensed under CC BY-SA 3.0 via Commons.
A blog about how music does that
- August 26, 2015
- By Dale McGowan
- In Intro
- 0
On September 1st, I’ll start a new blog here about music — not what it does to your brain, or how it can make your children brilliant or magically shrink your tumors, but the seldom-discussed fact that another person can make you feel intense and specific emotions, even take you through a changing emotional landscape, just by arranging sounds in a certain way.
I know how music does that. It’s the most interesting thing I know. I used to have a job teaching it, and after several years away, I’m ready to do it again.
I’ll start by walking through just enough music theory, then apply it to TV and film scores, classical, rock, and video game music, the strange startup music in my Nissan LEAF, the saddest piece ever written, the universal teasing song, and the interval British people use to say good morning when they don’t really want to talk to you.
While you’re waiting, you can learn more about how the blog will work, subscribe by email in the sidebar, and Like the blog’s Facebook page.
My Big Fat Christian Wedding
An ever-less-frequent series of posts while I’m working on a book about the secular/religious mixed marriage.
Deep into the wedding chapter now, including examples of the three general wedding flavors for secular/religious mixed couples: Sacred, Secular, and Swirl.
Mine was Type I, a traditional religious wedding. No one there would have guessed there was an atheist in the room, much less that he was the one in tux and tails. The setting was a beautiful, historic Lutheran church in San Francisco that we’d chosen not because it was Lutheran but because it was beautiful and historic and in San Francisco, Becca’s hometown.
We upped the religious ante with not one but two ministers–a Methodist friend of the family, and a Southern Baptist uncle of Becca’s whose contribution included a rafter-rattling reference to Matthew 21:21, the assurance that faith can move mountains. The readings were all Christian, ranging from the indispensable “love is patient, love is kind” from First Corinthians to a popular excerpt from The Prophet by the Christian mystic poet Khalil Gibran.
Ten years later, I’d have probably wanted to include some secular poetry or meditations and maybe nudged the scriptures a little — a nice humanistic bit from Ecclesiastes, say, instead of a verse on the telekinetic properties of faith.
But here’s the thing: At that point in my life, even though I was no less secular in my point of view, that played a much smaller part of my identity than it would later on. At 28, I was defined by music. My degrees were in music, and I was about to begin a 15-year career as a conductor and professor of music. I’d have been more offended by lame music than by all the Psalms in the KJV. It could rain little pillows embroidered with Proverbs for all I cared. The music was mine.
Included was Ravel’s Jeux d’eau and the “Menuet” from Sonatine, both played by my insanely talented brother Ron, plus Bach’s secular cantata “Sheep May Safely Graze,” a warhorse gone awesome in an arrangement for strings and two recorders. Becca entered to Bach’s “Air on the G String,” one of the most perfect things ever written, played by the San Francisco Conservatory String Quartet. We lit the unity candle to a prelude I wrote myself, also played by Ron, and we left to the ridiculously exuberant Widor Toccata for organ played by the organist of San Francisco’s Grace (Episcopal) Cathedral.
For those of you keeping score, we had now achieved the Protestant quadfecta: a Lutheran church, an Episcopal organist, and Methodist and Baptist ministers. I was awash in Christian ritual, text, and symbols — and I didn’t care a bit. I’d made my own heaven musically.
Are you in a secular/religious mixed marriage? This is the last week to submit your wedding story for possible inclusion in my book. Do it here!
